Date: Fri, 24 Jan 2003 13:22:38 -0500
Dear Bruno,
First let me state that the reason that I am discussing this idea with
you is so that I can "kill two birds with one stone". I would like to better
understand your thesis and would like to see how it accounts for or solves
the "epiphenomenona" problem so that I can evaluate a model that I am
working on.
----- Original Message -----
From: "Bruno Marchal" <marchal.domain.name.hidden>
To: "Stephen Paul King" <stephenk1.domain.name.hidden>
Cc: <everything-list.domain.name.hidden>
Sent: Thursday, January 23, 2003 2:18 AM
Subject: Re: "I" the mirror
> Hi Stephen,
>
> At 10:52 -0500 22/01/2003, Stephen Paul King wrote:
> >Dear Bruno,
> >
> > Thank you for the reference to the Case papers. It is ironic that
his
> >argument makes the case for the subtle issue that I am trying to point
out
> >to you, that there is a grave problem with your model.
> >
> > In http://www.cis.udel.edu/~case/self-ref.html we find a very
> >informative discussion of self-reference and the way that infinite
> >regression is avoided by using an "external" aspect to act as a
> >"mirror/sketch pad" for the machine to use as a self-referential imaging
> >system. While I do have some reservation regarding the assumption that
N ->
> >N functions can completely capture physics and the exclusive usage of
Well
> >founded statements in mathematics, I propose to set them aside for the
sake
> >of a discussion.
[SPK]
I have cut and pasted the exact words used:
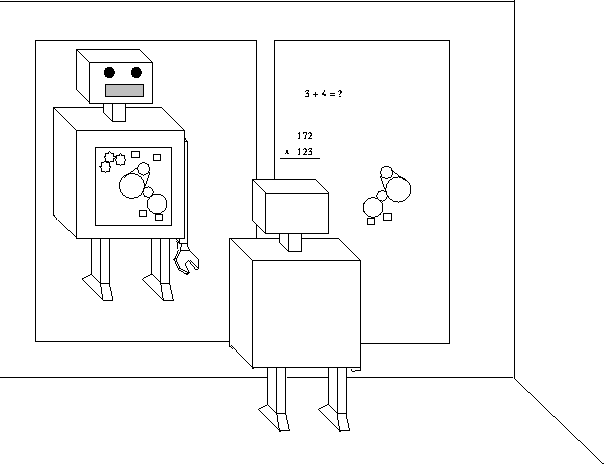
Machine Self-Reference
The robot pictured below has a transparent front and is facing an
(expandable) board, a little to its right, and a mirror, a little to its
left. It's transparent front enables it to see in the mirror its complete
underlying mechanism, flowchart, or program. The board serves for input,
output, and intermediate computations. Such a self-referential or
self-reflecting robot has data access, then, to a complete (low level) self
model.
It is depicted already having copied onto the board a portion of its
``program'' (corrected for mirror reversal). Note that the robot's self copy
is projected externally to the robot itself. In this way infinite regress is
not required for the robot to have complete (low level) self knowledge. The
use this robot makes of its complete (low level) self knowledge is whatever
was built into it, but it could have been anything algorithmic.
For general computer programs, in contexts where mirrors may not be
available, a quiescent (low level) self-model can be obtained by a mechanism
logically similar to the self-replication mechanism employed by
single-celled organisms.
>
> [BM] I am not sure which "external aspect" you allude to. Case'w work
relies
> on the second recursion of Kleene, which gives easy way to construct
> self-referential programs. The "mirror" is really in machine's head.
[SPK]
Ok, but if, as you state, the 'mirror' is really in the machine's head
we are only shifting the 3-person view; instead of seeing the robot standing
in front of a mirror, we zoom inside the robot's innards and find the
'mirror'. This does not chance anything.
On the other hand, you are making a different point since the 'mirror'
that Case and you (I think) are thinkng about is not a physical 'mirror' or
any other physical object. That is to be expected given that we seem to be
discussing the subtleties of an immaterail monist theory, but does nothing
to blunt the point of my question: Hw does an immaterial monist theory give
a consistent meaning to notions such as "transitivity", "concurrency",
"persistence" and other properties that are associated with physicality?
> The basic idea is very easy. Let D be a duplicator in the sense that
> the program D applied to X, written DX, gives a description of X apply to
> itself, that is XX.
> So DA gives AA. DB gives BB. DC gives CC, ...
>
> What gives DD?
>
> Yes. DD gives DD. It's an example of a duplicating program.
>
[SPK]
I have no difficulties with such notions, but would like to see a more
general situation discussed such as how we can have a formal model of
multiple 1-person intentionalities. I see this more general stuation as
being the exact analogy of the "problem of time" in physics and given my
interest in that problem I am engaging in this discussion. ;-)
> For all transformation T you can generalize and find a program which
> computes T applied to itself. Simple reproduction is the particular case
> when T = the identity transformation: take a new "duplicator" which
> apply to any X, written DX, gives T applied to a description of XX, that
> is T(XX). Now DD gives T(DD). DD gives T applied to itself.
>
> So you get self-referential machines by the substitution of some
> [variable of some transformation] by duplicator applied to themselves.
>
[SPK]
Ok, but where is the notion of "persistence" that is implicit in the
chain:
> take a new "duplicator" which
> apply to any X, written DX, gives T applied to a description of XX, that
> is T(XX). Now DD gives T(DD). DD gives T applied to itself.
There is obviously a transitive property here since we have to both
consider all of these machines, X, DX, T, XX, T(XX), T(DD) and DD as being
distinct from each others and yet have some relation between each other. If
we have a transitive relation or property, it seems necessary that there is
an assumption of persistence, even if it is that X = X for all instentional
statements s which are "about" X.
I see Kripke's "possible worlds" idea to be the first explicit
elaboration of this notion that I am trying to discuss and it is implicit in
all philosophical discussion of "objects" even if they are considered as
"immaterial". We have to assume some basis set or class and it seems that
the property of "persistence" is tacitly assumed for such. But what I am
trying to point out is that persistence as implied by the formal statements
of "X exists" does nothing to "substantiate" (Literally!) those statements
and "transitivity", such as implied by statements such as your here, are a
related but different property. Both need to be, at least, accounted for in
our models.
> You could say that the self-referentiality comes from the language
> chosen, but working with Rogers numerical representations, the \phi_i,
> you can show the reasoning constructive and machine, or programming
> language, independent.
>
> What remains true is that any self-referential program needs a universal
> program to run it, for making the self-referentiality manifest.
> I have never deny that.
>
[SPK]
Ok, I am not questioning whether or not there "exists" self-referential
programs (plural???) or a "Univiversal program" (singular???), I am
wondering about how do we go from formal existence postulation to the
possibility of "maniferstation" itself. This is where I think that there is
a problem if only in that the domain of explanatory power of such models
only applies to a very narrow range. Here we find the following:
http://www.cis.udel.edu/~case/slides/krt-consc-cs-slides.ps
page 6. (I hope that my correctiond for LaTex are correct.)
***
Fix a standard formalism for computing all the (partial) computable
functions mapping tupes
from N (the set of nonnegative integers) into N . Code number the
programs/machines in
this formalism onto N. Let \Delta p( . , ... , .) be the (partial) function
(of the indicated number of
arguments) computed by program number p in the formalism.
Kleene's Theorem
(\forevery p)(\thereexist e)(\forevery x) [\Delta e(x) = \Delta p(e, x)].
p plays the role of an arbitrary preassigned use to make of selfmodel. e is
a selfknowing program/machine corresponding to p. x is any input to e.
Basically, e on x, creates a self copy and, then, runs p on (the selfcopy;
x).
In any natural programming system with efficient (linear time) numerical
coding/decoding of programs, passing from
any p to a corresponding e can be done by a linear time algorithm;
furthermore, the resultant e itself efficiently runs in time
O(the length of p in bits + the run time of p)
***
We notice that the domain and range of the functions is N (the set of
nonnegative integers), thus it is being assumed that this model that only
uses N -> N functions can give us a model of "self-reference" that is
sufficient to, at least, avoid the infinite regress that in implicit in the
usual notion of machines creating models of themselves.
What I understand of this is that we are intentionally limiting the
class of functions and the domain and range so that the infinite regress
does not occur. It is additionally interesting to notice a pair of
statements that Case makes on page 3 of the above mentioned paper:
"Infinite regress! M inf. hence M not a machine."
"therefore M can not contain a model of itself"
This notion of "containment", in itself, begs the question that I am
asking!
> What the universal dovetailer argument shows is that from the
> point of view of the machine, if she looks closely enough to its probable
> local implementation, that is near its comp substitution level, she will
> describe not one universal machines, but MANY one.
>
[SPK]
Exactly what is the formal statement of "if she looks closely enough to
its probable local implementation" or equivalently, "near its comp
substitution level"? Are you assuming some kind of "delta-epsilonics" here?
I still do not understand how you go from UDA to 1-uncertainty. Please
point me to the definitions again. ;-)
> QM confirms that. But people have invented selecting rules, like
> the collapse of the wave or some guiding potential, making things look
> more Aristotelian. But Everett comes and said "why for?".
>
[SPK]
Hold on! The "collapse of the wave function" is introduced to try to
explain the disparity between the non-distributive and non-Boolean aspect of
QM and the logic implicit within individual 1-person experiences. QM has
been compared by David Finkelstein to a relativity of experiments, where
there does not exist an absolute universal experiment.
As I re-read D. Finkelstein's essay: Finite Physics, it seems that what
you and other computationalist are proposing is identical to that Prof.
Finkelstein is trying to generalize:
"An abolute or nonrelativistic physics ... postulates
1) a universal experimental language,
2) a universal experiment, and
3) a universal experimental subject.
The universal experiment is the simultaneous determination of all the
variables of the system. The universal subject is the universe itself. Both
figure explicitly, fdor example, in Laplace's fantasy of the intelligence
who knows all and does nothing."
It is easy to see the analogy!
> And I come, if you want, and just say that if you take seriously the
> Everett comp then you can ask "why for?" even for the Schroedinger
Equation.
>
[SPK]
I would kindly submit that neither you not I understand exactly what the
SWE is, but to say that Everrett's comp idea exists without SWE is absurd!
It is the SWE that defines the "thereexist X" postulation of the "relative
states" that are considered as "worlds" or "minds" or "histories", etc. ,
such that without X being assumed to exist the notion of self-aware entities
of self-referential systems is meaningless noise, at best!
> Not because you should dismiss it, but because if it is true, it should
> be derivable from LOGIC + ARITHMETIC. That the result of the UDA proof.
[SPK]
I do not dispuse "LOGIC + ARITHMETIC". I am just wondering how it is that
you can assume that LOGIC + ARITHMETIC can be meaningfull and persistent
entities without having to deal with the obvious infinite regress that is
entailed. If there is no "externality" upon which to mirror internal
properties, how do you avoid the regress?
BTW, I like the idea of using non-well founded set theory because in it
infinite regression and circularity are not problematic at all, but the nice
and neat notions inplicit in Church-Turing thesis vanish.
>
>
> >SPK:
> > Your model, as I understand it, ...
>
> BM:
> But I'm afraid you miss the point. It is not a "model". It is not
> a theory.
> It is a "theorem", a deductive argument. If you don't understand it,
> you should tell me at which step of the reasoning you are stuck.
>
[SPK]
Even so, the theorem is based on an assumption!
> I am not so interested in knowing if the hypotheses are true. I am
> enough glad for showing them refutable.
>
> When a computationalist practitioners accepts an artificial digital
> brain, he does not ask for a model in its head. He asks and hope for
> the real thing.
>
[SPK]
There is no clear evidence that a digital emulation of brain activity
will have an analogous digital 1-person associated. The strong AI hypothesis
is merely that, a hypothesis. I am remined of the discussion that some have
made regarding a book within which a complete description is written of
Einstein's brain. Is it assumed that the mere enumeration, assuming
enumerability, of the states of Einstein's brain is enough to give us a
1-person existence of Einsten? This is silly at best!
> In case he survives (= COMP) he can bet he is immaterial. He can choose
> is body and travel on the nets, without any stable body. The UDA result
> is that this imateriality is contagious, in some sense, the environment
> cannot be more material than himself. Descartes, Hume, and Kant have
> partially describe this.
>
[SPK]
What I am pointing out is that you are assuming at least the possibility
of an "embodiment", even if there does not exist a single stable "body". We
can extend the Einstein book to a data base that is continuously circulated
between servers on the internet, but the question remains, unless the
possibility of a physical server with some non-zero persistence of "being"
is assumed, even the notion of an Einstein data base becomes impossible.
This exposes a problem deeper than that of the causal non-efficasy of
"matter" within a immaterial monist theory!
It boils down to saying that you can not postulate your cake and eat it
too!
>
> SPK:
> >would seem to make the "mirror/ sketch
> >pad" to be a derivative or "epiphenomenona" of the UD,
>
>
> BM:
> Why epiphenomena? They are phenomenal appearances, stable patterns in
> consistent machines memories. Dreams if you want, but stable
> dreams in which they have partial control ...
[SPK]
What does the word "stable" mean in your thinking here?
> And thanks to the G/G* difference we get communicable and
> incommunicable truth. Thanks to the Z/Z* difference we get
> room for both physical measure and physical sensations, as
> uncommunicable physical result of (self)measurement.
>
>
> SPK:
> >e.g. that physicality
> >itself is merely derived from the intetionality of arithmetic statements,
>
> BM:
> Yes.
>
[SPK]
Ok, well how do we go from intesionality to persistence such that a
3-person view is even possible?
> SPK:
> >what x implies about y. My argument is that if physicality is mere
> >epiphenomenona, is it sufficient to merely have a "belief" by S that x
> >implies y to have a causal consequence on the possible behavior of S,
such
> >that if x did not imply y behavior would be 3-person distinguishable?
>
> BM:
> ... would be 1-person plural distinguishable (for the technical reason
> that the quantum, seems to appear at the star level. I am not yet sure).
[SPK]
I hope that you can explain this further soon!
> But you are right. That is, if that is believable and consistent.
> It is not that mind acts on matter, but it is more like the arithmetical
> border of mind defines matter. Roughly speaking.
>
[SPK]
How is this "arithmetical border of mind" any different from the
Cartesian cut, the distiction between subject and object?
> SPK:
> > What I seem to be getting at is how do you relate 1-uncertainty to
> >3-person belief? I see the paper by Pratt that I have mentioned before
makes
> >some headway on this question, but have not seen any of your comments
about
> this.
>
> BM:
> We will come back later on Pratt. It is very technical and he redefined
> mind and body in a very special sense. I guess something interesting. We
will
> see if it helps for the Z1(*) semantics ...
[SPK]
I am very eager to see this!
> Don't hesitate to send a readable description of Pratt's "headway"
> for us all, anyway. Explain perhaps enough for explaining the subtle point
> which, if I understand you, would make comp inconsistent, or perhaps
trivial.
>
[SPK]
Ok, it seems that this is inevitable, but you realize that if a person
that is familiar with computer science, such as yourself, is having
difficulties understanding Pratt's paper, imagine the mere amateur such as
myself! I find this incredible! Is there nothing in his paper that gives you
a "toehold" on what he is talking about? BTW, you are not the first to not
understand his idea! I have tried to engage Pratt directly in a discussion
of his paper and so has Peter Wegner, but he seems to not be willing to do
so for some reason.
Since so much of my own idea depends on Pratt's notions, I will try to
produce a "readable description", but it will take some time and effort.
Kindest regards,
Stephen
(image/gif attachment: sr-robot.gif)