Date: Wed, 5 Apr 2006 12:12:07 +0200
Le 04-avr.-06, à 20:11, daddycaylor.domain.name.hidden a écrit :
> Bruno,
>
> To help us understand this: How is this different from saying the toss
> of a coin is both unpredictable and yet determined by laws?
I guess the unpredictability of the coin can be of the type of
"determinist chaos".
Of course, if you manage to tossle the coin enough, Heisenberg quantum
"error" will add and you will find yourself differentiated in a
continuum of worlds with "head" and a continuum of world with "tails".
To relate it to "number theoretical sort of indeterminacy" is very
difficult, and bound up to rely on unsolved conjectures. Grosso modo
"primes indeterminacy is related to Riemann Hypothesis". Experimental
evidence obtained from heavy computation confirmed the feeling. Then
diagonalization à-la-Godel can relate degrees of indeterminacy and
numbers, but without providing information on "real-math" sort of
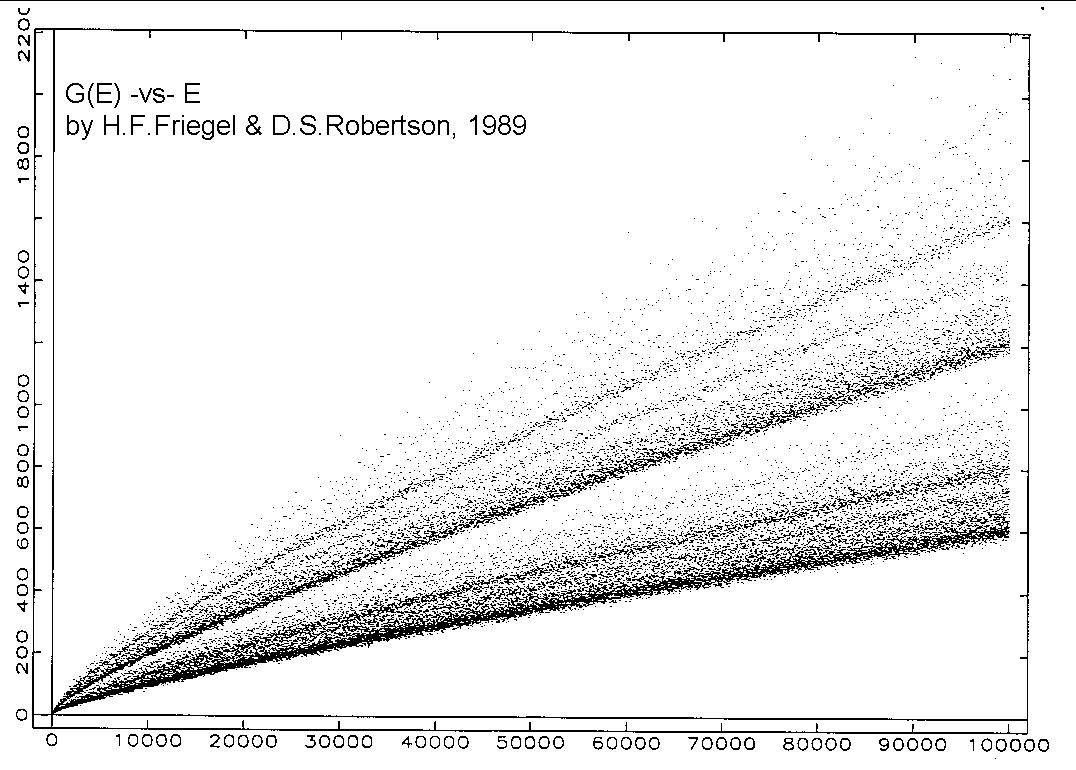
indetermination. Look on the net for the "Goldbach comet" for an nice
"experimental evidence" for the rise chaos in number theory. Here:
--~--~---------~--~----~------------~-------~--~----~
You received this message because you are subscribed to the Google Groups "Everything List" group.
To post to this group, send email to everything-list.domain.name.hidden
To unsubscribe from this group, send email to everything-list-unsubscribe.domain.name.hidden
For more options, visit this group at http://groups.google.com/group/everything-list
-~----------~----~----~----~------~----~------~--~---
Taken from: http://www.primepuzzles.net/puzzles/puzz_082.htm
(In case your mailer does not support image).
>
> Another thought is that there are the two extremes of the meaning of
> "law":
>
> 1) The reductionist definition that something can be predicted by the
> sum of atomic parts and rules.
> With the primes it is the integers and addition and multiplication.
> With a coin supposedly it is "atoms" and the laws of physics.
> 2) The statistical definition that something follows a certain
> distribution over many trials.
> With the primes it would be the prime number theorem or more precise
> bounds on the distribution of the primes. With a coin it would be the
> binomial distribution.
>
> This brought up another thought. The definition of the primes is a
> negative definition, an integer having no factors other than 1 and
> itself.
It is a negative definition bearing on something finite, so I am not
convinced. You can also transform it into a positive definition:
p is prime if for any number x, if x divides p then x is equal to 1 or
x is equal to p.
> Of course this is what makes it difficult to determine if a
> large number is prime. But is there something about a negative
> definition that sets us up for... what... not being able to understand
> something? This also reminds me of the diagonalization process,
> defining something by saying it is not something else, like Chaitin
> does with his Omega, and of course Cantor with the reals (resulting in
> the mystery of the continuum hypothesis). Another famous negative
> definition is that of infinity, which causes so many weirdnesses in
> divergent series, and talking about the multiverse, etc.
There are too many things here. I will say more on diagonalization in a
post to answer George Levy's question in the everything-list.
>
> Perhaps free will is such a mytery because it can be defined only
> negatively. Free from what?
It is like in the so called (neoplatonist) negative theology. I follow
your intuition that "big and complex" things need to be defined
negatively. In the field of computer science this has been made
possible through Church Turing Thesis. To show that a function is
computable, you need only to give reasonably clear instructions for
computing it. To prove that a function is NOT computable, you need to
choose a formal definition of computability, and the "uncomputability"
will make sense only if the definition of computability you chose
encompass all possible notions of computations (which is implied by
Church Turing Thesis). Karl Popper did make an attempt to explain
free-will in term of "self-diagonalization" indeed. The basic and
simple idea is that IF I can totally predict myself, then I have the
opportunity to refute such a prediction. This is why in a trial your
lawyer cannot invoke determinacy (like my client has made a murder, but
really he was just obeying to the physical laws), because if such a
determination can make sense then the "client" could have use in some
responsible way to escape its murderer fate still without violating the
physical laws. I don't pretend there is any rigor here.
"Free from what?": Free from what you can determine. The one who can
determine that heavy bodies fall, will soon or later be able to fly.
Bruno
http://iridia.ulb.ac.be/~marchal/
(image/jpeg attachment: Gcomet.jpg)