Date: Wed, 29 Mar 2006 18:26:21 +0200
Hi,
I think I have already mentionned it (four years ago?) but I have
another Theory of Everything sleeping somewhere in my brain and books.
I made an allusion about it yesterday in my post to Peter D Jones, and
I take this as an opportunity to say some more words on it. Hope it is
not too technical.
That theory is hardly original because it simply corresponds to the
Polya-Hilbert conjecture in number theory. To sum it up, Euler
discovered a rather cute relationship between the infinite sum of the
inverse of natural numbers, with some exponents, and some infinite
products related to the prime numbers. Precisely:
Sum (n = 1 to infinity) 1/n^s = Product (on all primes) 1/(1-1/p^s).
This is the well known zeta Riemann function.
If you can read html:
--~--~---------~--~----~------------~-------~--~----~
You received this message because you are subscribed to the Google Groups "Everything List" group.
To post to this group, send email to everything-list.domain.name.hidden
To unsubscribe from this group, send email to everything-list-unsubscribe.domain.name.hidden
For more options, visit this group at http://groups.google.com/group/everything-list
-~----------~----~----~----~------~----~------~--~---
Or look at http://primes.utm.edu/notes/rh.html
or here: http://www.maths.ex.ac.uk/~mwatkins/zeta/tutorial.htm
The equivalence of that sum and product is actually equivalent with the
fundamental theorem of arithmetic (which says that all numbers admit a
unique decomposition in a product of primes numbers (not taking into
account the factor order). Thanks to the work of Cauchy (complex
analysis) Riemann realized that his zeta function zeta(s) defined a
unique analytical function from C to C (C = the complex numbers), that
is taking s as a variable on the C complex plane.
Zeta(1), which is the harmonic series, still diverge but all other
value of s, crazily enough, makes zeta converging. In particular
zeta(-1) = -1/12. And this is a little bit crazy because it means that
on the complex plane there is a sense to say that the infinite serie 1
+ 2 + 3 + 4 + 5 + ... converge to minus 1/12. (When Ramanujan applied
for a mathematician job in England, he just annonce that formula to
show that he has some ability in computation stuff, and then he has
been lucky enough that Hardy did understood it at once, knowing Riemann
work).
Now some computation can show that the behavior of the prime numbers, I
mean the way they are distributed among natural numbers, is controlled
by a set of zero of the Riemann zeta function.
Actually that control is very fine once we assume those critical zero
are all arranged on a line, and this is the famous Riemann hypothesis
which fascinates so much mathematicians. The best introduction to that
field (for those who remembers their high school math) is the dover
book:
H. M. Edwards, Riemann's Zeta Function, Dover Publications, 2001. It
contains the original paper by Riemann.
Now, all those zero could be justified being on a line in the case
those zero would describe a spectrum of some quantum observable, and so
this suggests a way to tackle that conjecture, and that way is
attributed to Polya and Hilbert---from oral talks, see:
http://www.dtc.umn.edu/~odlyzko/polya/index.html
Now a logician can show that if you take the arithmetical formula
having only the addition symbol (together with all other logical
symbols except the multiplication) or, contrarily, only the
multiplication symbol (and the logical one but no addition) well, in
each case you can find a corresponding decidable and complete theory
(with respect to truth for those set of formula).
Put in another way, it is the mixing of addition and multiplication
which is at the original of the richness of the relation between
numbers. I have always suspected that the distribution of the prime
numbers could encoded the logical mess coming from that mixing. In that
case some "total" knowledge of the distribution of the primes would
encode a necessarily non trivial part of the (incomplete,
unaxiomatizable) arithmetical knowledge.
The fact is that, thanks to an algorithm due mainly to Turing and
refined by Odlyzko, there is a sort of experimental verification of the
Polya-Hilbert conjecture. Indeed it looks like if the zeros of the zeta
function describe a spectrum already introduced by quantum physicists
when they have been confronted to very complex quantum system like big
atom's nucleus: actually they introduce for such system just very big
random matrices up the necessary condition of being unitary. It can be
shown that such operator (interpreted in some way) describes a form of
"quantum chaos". Such an "experimental" verification is of course very
frustrating from the point of view of a mathematician who want to
*prove* the Riemann hypothesis, but then it is a sort of delight for a
pythagorean philosopher who want to extract physics from number theory.
Actually, assuming comp and the 1-3 distinction, it would be enough to
show that this "quantum chaos" (or some semi-classical regime which can
be associated with it) is rich enough to simulate (even in a weak local
sense) a universal dovetailer, for getting freely a universal quantum
dovetailer from the prime numbers.
I believe that an extraction of a universal dovetailer from the primes
would also make the Riemann hypothesis undecidable in a very weak
arithmetical theory (like Peano Arithmetic, or the weaker Robinson
one), and that would be enough to prove the Riemann hypothesis (giving
that if the Riemann Hypo is false then it is refutable in Peano
Arithmetic (because PA can provably simulate the Turing-Odlyzko
algorithm which search for zero out of the critical line).
Such a theory is obviously compatible with what we could find by the
"pure" interview of the lobian machine, and if it is true, should be
identical.
Such a Pythagorean TOE would give a more direct explanation of physics
from numbers, as compared to the lobian interview which needs that
godel encoding of propositions and machines, in term of numbers (many
mathematicians hates such (intensional) use of numbers), but then such
a theory would hide the 1-3 distinction in some "Everett like
interpretation of prime number generated quantum chaos).
Unfortunately I don't know well about quantum chaos. If someone knows
about a proof of non-universality of quantum chaos .... Actually I got
a proof of turing universality of classical chaos, and I got evidence
of many universal facets of the zeta riemann conjecture, thanks to a
work by Voronin:
http://www.maths.ex.ac.uk/~mwatkins/zeta/voronin.htm
The rest are conjectures; even more difficult than the lobian one ...
Still I hope this post can help you to understand in a different way
than my usual UDA/Lobian one, (or Hal Finney's universal absolute
distribution, and other OM based toes) how realities could emerge from
number theoretical relations. The advantage is that if it works, it
would provide directly a universal *quantum* dovetailer. The lobian one
leads only indirectly to it (if it leads to it at all).
Bruno
http://iridia.ulb.ac.be/~marchal/
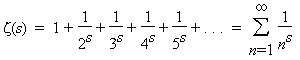
(image/gif attachment: zetafun1.gif)

(image/gif attachment: zetafun2.gif)